Researchers from Skoltech, the University of Arizona and Linköping University in Sweden have created a graphical model that describes the patterns of infection outbreaks spreading between different localities. The model helps calculate the probability of a selected group of areas being hit by a local outbreak and map out a minimum set of prevention measures. The paper was published in Scientific Reports.
Predicting the COVID-19 spread patterns still remains an unresolved issue. The recent series of hard-to-predict COVID-19 outbreaks underscores the importance of modeling and prediction. However, the modeling encounters two stumbling blocks: first, it involves calibration of an enormous number of parameters based on data and, second, models with too much detail and carefully selected parameters turn out to be impractical for predicting the spread patterns and selecting the prevention strategies. That said, for the modeling to be effective, the model should not be crammed with detail in order not to complicate calculations but be detailed enough to enable predicting the spread dynamics and working out the containment strategies.
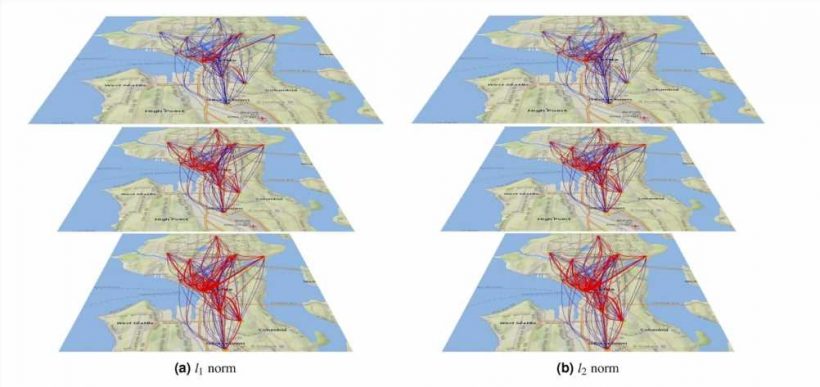
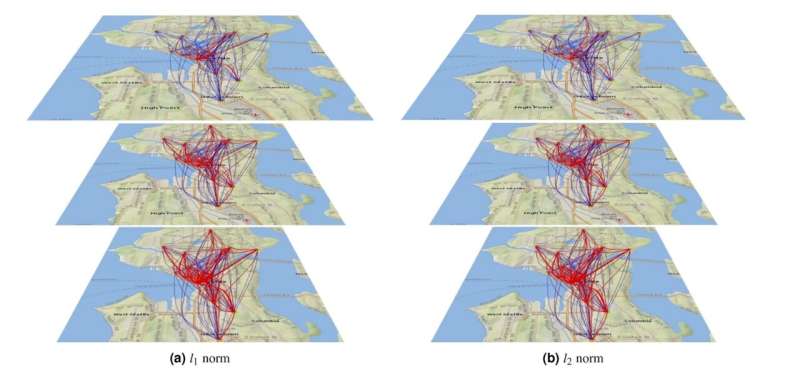
One way to model the spread of outbreaks is probabilistic graphical models, where each vertex represents a populated area and the ribs show the probability of a node getting the infection from the neighboring node. For example, the greater the population flow between areas, the higher the chances of the outbreak moving from one area to another.
In their recent study, the researchers turned for the first time to probabilistic graphical models to solve a two-level task and answer two questions: how does an outbreak spread from a vertex, and what are the minimum steps that would prevent the infection from sprawling all over the graph?
“Our team of experts in applied mathematics that makes part of a larger multidisciplinary group has been modeling the pandemic for over a year. We use models from the realm of physics to pin down the most likely post-infection state of the system and prevent further spread. Since any restriction has cost implications, we wish to achieve the utmost effectiveness of containment with a minimum of interventions,” the first author of the paper, Skoltech Ph.D. program graduate Mikhail Krechetov, says.
In their study, the researchers used the mathematical apparatus of statistical physics, namely, the Ising model that describes the material magnetization process. In the team’s model, the graph nodes represented city districts and the ribs the traffic between them. Also, the infection probability calculations took into account the prevention factors, such as masks, social distancing, vaccination coverage, and the like.
To bring the model as close to reality as possible, the team used real data from Seattle (WA, U.S.A.) and mobile tracking data on population flows between areas.
First the researchers checked which nodes would be the next to catch the infection from the infected node and then figured out what minimum number of steps is needed to curb the spread. They showed that the model helps define transportation restrictions in the case of an outbreak in a specific area and make sure other areas do not become infected. Moreover, graphical models proved to be helpful in solving the same task for any number of affected locations.
“Our model is universal as regards its graph topology, and the method works well even for very dense graphs describing cities with massive inter-district population flows. However, the spread patterns and restrictive strategies in dense graphs turn out to be totally different from those in sparse graphs with less intensive migrations. An interesting mathematical implication for us is how the choice of the function for cost estimations influences the solution’s structure: one case requires pointwise but more significant traffic adjustments, while the other needs small but evenly distributed changes,” Mikhail adds.
Source: Read Full Article